Algorithm
- Finite set of computational instructions
- Set of steps to solve the problem
Properties:
- Input / output : some input from some standard set of input and must produce output
- Definiteness: each step must be unambiguous
- Finiteness: algorithm must terminate after finite tome or steps
- Correctness: correct set of output values must be provided from each set of inputs
Random Acess Machine Model
- Base machine model for the study of design and analysis of algorithm
- Machine independent environment
- Each basic operation (+, -) takes steps
- Loops and subroutines are not basic operations
- No shortage of memory
E.g
Fibonacci(n)
{
a=0; b-1, f=1;
for(i=2; i<=n; i++)
{
F=a+b;
A=b;
B=f;
}
return f;
}
GCD (Greatest Common Divisor)
- Common method to calculate GCD
GCD (4,8)
4=2*2*1
8=2*2*2*1
GCD (4,8)= 2*2*1 =4
- Euclidean algorithm to find GCD
GCD(a,b)
{
If (b==0)
Return a;
Else
Return GCD (b, a mod b)
}
Case 1:
No. of basic operation (division)=5
Case 2
No. of basic operation = 2
Asymptotic Notation
Mathematical notations which are used to describe running time of algorithms
- Complexity analysis of the algorithm is very hard if we try to analyse the exact; so its nearby solution
- the complexity of an algorithm is the mathematical function of size of input
- So we analyze the algorithm in terms of upper bound and lower bound
- Mostly we concentrate on worst case only
- Check image [graph wala]
- Three types of asymptotic notation
- Big Oh (O) Notation
- Big Omega (Ω) Notation
- Big Theta (Ꝋ) Notation
Exponents
xaxb=xa+b
…
Check photo
Logarithms
- Logab= loaga+logb
- Log(a/b)= loga-logb
- Log (ab) = bloga
- Log1=0; log2=1; log1024=10
Series
See photo
Big Oh (O) Notation
- A function f(x)=O (g(x)) iff there exists two positive integers c and no, such that for all n>=no, 0<=c*g(n)<=f(n)
- Represents the upper bound of the running time of an algorithm
- Worst-case complexity of an algorithm can be found with big oh
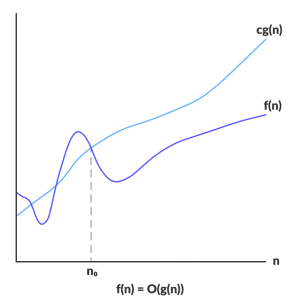
Credit: https://www.programiz.com/
e.g
f(n)=3n2+4n+9
g(n)=n2
Prove that f(n)=O(g(n))
= O(n2)
Big Omega (Ω) Notation
- A function f(x)=Omega(g(x)) iff there exists two positive integers c and no, such that for all n>=no, 0<=c*g(n)<=f(n)
- represents lower bound
- gives best case of algorithm
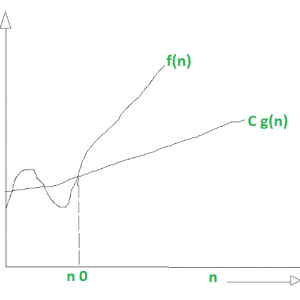
https://www.geeksforgeeks.org/
Big Theta (Ꝋ) Notation
- A function f(x)= Ꝋ (g(x)) iff there exists three positive constans c1, c2 and no, such that for all n>=no, 0<=c1*g(n)<=f(n)<=c2*g(n)
- See photo
Difference between big oh, big omega and big theta
Example (Insertion Sort)
For (i-1; i<n; i++)
{
X=A[i];
j=i-1;
while(j>=0 && A[j]>x)
{
A[j+1]=A[j];
j=j-1
}
A[j=1]=x;
}
To be continued…
Table xa
Time Complexity





