- p/q p, q R, is undefined if
(a) p 0, q = 0 (b) p = 0, q = 0
(c) p 0, q 0 (d) p = 0, q 0
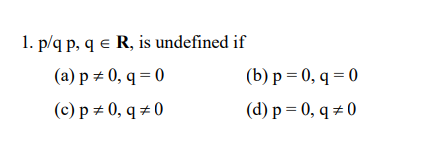
The expression p/q, where p and q are real numbers, is undefined if:
(a) p ≠ 0 and q = 0
In this case, when the numerator (p) is nonzero and the denominator (q) is zero, the division is not defined because division by zero is undefined in mathematics.
The options (b) p = 0, q = 0 and (c) p ≠ 0, q ≠ 0 are not the correct conditions for the expression to be undefined. In the first case, if both the numerator and denominator are zero, the expression would be considered as 0/0, which is an indeterminate form. In the second case, if both the numerator and denominator are nonzero, the expression is well-defined.
Therefore, the correct answer is (a) p ≠ 0, q = 0.
2. [a, b] = (a) {x : a x b} (b) {x : a < x < b} (c) {x : a < x b} (d) { x : a x < b}
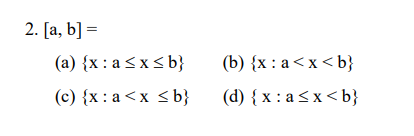
The notation [a, b] represents a closed interval, which includes both endpoints a and b. The correct representation of the closed interval [a, b] is:
(a) {x : a ≤ x ≤ b}
Option (a) correctly represents the interval [a, b] as the set of all x values such that x is greater than or equal to a and less than or equal to b. This notation includes both endpoints a and b.
Options (b), (c), and (d) do not accurately represent the closed interval [a, b]. Option (b) represents an open interval, (c) represents a half-open interval, and (d) represents another type of half-open interval.
Number of nonempty singleton subsets from the elements of the set {l,m, n, p} is
(a) 4 (b) 3 (c) 2 (d) 1

The set {l, m, n, p} has four elements. A nonempty singleton subset is a subset that contains only one element.
To find the number of nonempty singleton subsets, we count the number of individual elements in the set. In this case, there are four elements: l, m, n, and p.
Therefore, the number of nonempty singleton subsets is equal to the number of elements in the set, which is 4.
So, the correct answer is (a) 4.
Let f : AB, then f is invertible if
(a) f is one-one (b) f is onto
(c) f is both one-one and onto (d) f is one-one into

A function f : A → B is invertible if it is both one-to-one (injective) and onto (surjective).
One-to-one (injective) means that each element in the domain A maps to a unique element in the codomain B. In other words, no two distinct elements in A can have the same image in B under the function f.
Onto (surjective) means that for every element in the codomain B, there exists at least one element in the domain A that maps to it. In other words, the range of the function f covers the entire codomain B.
So, the correct answer is (c) f is both one-to-one and onto.




